Sistem Persamaan dua variabel (peubah) atau disingkat SPLDV adalah suatu persamaan
matematika yang terdiri atas dua persamaan linear yang masing-masing
bervariabel dua (misal x dan y). Dengan demikian, bentuk umum dari Sistem
Persamaan Linear Dua Variabel dalam x dan y dapat kita tuliskan sebagai
berikut.
ax + by = c
|
atau
|
a1x + b1y = c1
|
px + qy = r
|
a2x + b2y = c2
|
Sistem Persamaan dua variabel merupakan
pelajaran matematika dasar SMP yang sebenarnya mudah tapi akan terasa susah
apabila kita tidak mengetahui cara menyelesaikannya.
Oleh karena itu pada kesempatan yang berbahagia ini mari kita cermati Bersama cara menyelesaikan soal system persamaan dua variabel.
Berikut ini adalah 3 cara atau metode yang cukup familiar untuk menyelesaikan kasus-kasus SPLDV, yaitu;
Oleh karena itu pada kesempatan yang berbahagia ini mari kita cermati Bersama cara menyelesaikan soal system persamaan dua variabel.
Berikut ini adalah 3 cara atau metode yang cukup familiar untuk menyelesaikan kasus-kasus SPLDV, yaitu;
1. Metode grafik
Penyelesian sistem persamaan linier dua variabel pada cara grafik
adalah perpotongan dua garis.
Contoh:
Tentukan penyelesaian sistem persamaan linear 2x + 3y = 6 dan 3x - y = -2 dengan metode grafik!
Jawab:
Gambarlah grafik masing-masing persamaan pada salib sumbu yang sama, yaitu :
Contoh:
Tentukan penyelesaian sistem persamaan linear 2x + 3y = 6 dan 3x - y = -2 dengan metode grafik!
Jawab:
Gambarlah grafik masing-masing persamaan pada salib sumbu yang sama, yaitu :
Kedua garis tersebut berpotongan di
titik (0,2).
Jadi (0,2) adalah satu-satunya pemecahan masalah dari sistem persamaan linear dengan dua peubah tersebut.
Atau bisa dikatakan (0, 2) adalah akar dari sistem persamaan linear dua variabel.
Jadi, nilai x = 0 dan nilai y = 2.
Jadi (0,2) adalah satu-satunya pemecahan masalah dari sistem persamaan linear dengan dua peubah tersebut.
Atau bisa dikatakan (0, 2) adalah akar dari sistem persamaan linear dua variabel.
Jadi, nilai x = 0 dan nilai y = 2.
2. Metode Eliminasi
Cara eliminasi dilakukan dengan
menghilangkan salah satu variabel secara bergantian
Contoh soal:
Perhatikan koefisien-koefisien variabel x dan y dari sistem persamaan linear berikut dan jawablah menggunakan metode eliminasi!
Contoh soal:
Perhatikan koefisien-koefisien variabel x dan y dari sistem persamaan linear berikut dan jawablah menggunakan metode eliminasi!
Jawab:
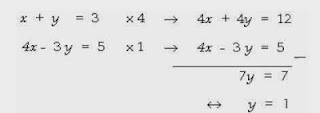
Diawalii dengan penyamaan koefisien
pada variabel x, yaitu:
Diakhiri dengan penyamaan koefisien pada variabel y, yaitu:
Jadi, penyelesaian dari persamaan tersebut di atas adalah x = 2 dan y = 1, dan himpunan penyelesaiannya adalah {(2,1)}.
3. Metode Subsitusi
Cara substitusi dilakukan dengan
menyatakan salah satu variabel dalam variabel yang lain kemudian memasukkannya
(mensubstitusikan) pada persamaan yang lain.
Karena secara bahasa subsitusi artinya mengganti, maka dapat pula diartikan bahwa metode subsitusi adalah menggantikan variabel yang kita pilih pada persamaan pertama dan digunakan untuk mengganti variabel sejenis pada persamaan kedua.
Contoh:
jawablah persamaan di bawah ini menggunakan metode subsitusi.
Karena secara bahasa subsitusi artinya mengganti, maka dapat pula diartikan bahwa metode subsitusi adalah menggantikan variabel yang kita pilih pada persamaan pertama dan digunakan untuk mengganti variabel sejenis pada persamaan kedua.
Contoh:
jawablah persamaan di bawah ini menggunakan metode subsitusi.
Jawab:
Semoga cara ini bermanfaat buat kamu yang sedang mempelajari system persamaan dua variabel ataupun buat kamu yang mau lagi ulangan ujian san sebagainya.













0 komentar